What Is Commutative Law Of Vector Addition Class 11
It is further clear that the order of vectors in vector addition is immaterial. If θ is the angle between and then the magnitude of the resultant vector will be R A 2 B 2 2AB cos θ.
The addition and subtraction of vector quantities does not follow the simple arithmetic rules.
What is commutative law of vector addition class 11. It is important to realize that a vector space consisits of four entities. This law is also referred to as parallelogram law. Addition is commutative meaning that one can change the order of the terms in a sum but still get the same result.
44c the same vector R is obtained. Commutative law and associative law. After understanding what is a vector lets learn vector addition and subtraction.
Image to be added soon. Finite angular displacement is a pseudo vector scalar as for large values of θ the commutative law of vector addition is not valid. So vector addition is commutative.
Commutative Law - the order in which two vectors are added does not matter. Infinitesimal small angular displacement is a vector quantity. Euclid built all of mathematics on these geometric foundations going so far as to define numbers by comparing the lengths of line segments to the length of a chosen reference segment.
104 Addition of Vectors. Consider the two vectors again. For the addition of vectors you have two laws.
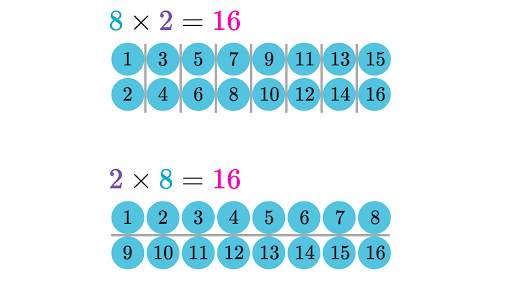
The fact that addition is commutative is known as the commutative law of addition or commutative property of addition. Vector Addition and Subtraction. Now for using the parallelogram law we represent both the vectors as adjacent sides of a parallelogram and then the diagonal emanating from the common point represents the sum or the resultant of the two vectors and the direction of the.
Tan-1 A sinθBA cosθ. Following are some points to be noted while adding vectors. Thus vector addition is commutative.
Is the angle between and then. A set of scalars. In this article we will look at the scalar or dot product of two vectors.
Symbolically if a and b are any two numbers then a b b a. In ancient Greek mathematics space was a geometric abstraction of the three-dimensional reality observed in everyday life. Vector addition follows two laws ie.
The result of adding vectors A and B first and then adding vector C is the same as the result of. We have already studied about the addition and subtraction of vectorsVectors can be multiplied in two ways scalar or dot product where the result is a scalar and vector or cross product where is the result is a vector. If we find the resultant of B A as in Fig.
A set V of vectors. This law is also very similar to the triangle law of vector addition. According to this law the initial point of one vector should coincide with the terminating point of the other vector.
Consider a parallelogram two adjacent edges denoted by. The Statement of Parallelogram law of vector addition is that in case the two vectors happen to be the adjacent sides of a parallelogram then the resultant of two vectors is represented by a vector. Later on this could be the set of complex numbers C A vector addition denoted by.
About 300 BC Euclid gave axioms for the properties of space. Triangle Law of Vector Addition. A special set of rules are followed for the addition and subtraction of vectors.
Furthermore this vector happens to be a diagonal whose passing takes place through the point of contact of two vectors. A B B A 41 The addition of vectors also obeys the associative law as illustrated in Fig. In this class it will alawys be the set of real numbers R.
4The rate of change of angular displacement wrt time is called angular velocityIt is given by 6.
Commutative Property Of Multiplication Review Article Khan Academy
